Karl Weierstraß und sein unendlich struppiges Monster
Die Forschungsergebnisse und -methoden von Karl Weierstraß sind fundamental für den Wissenschaftszweig Mathematik – für das Schulfach Mathe weniger. Doch zumindest ein Hauch seiner sprichwörtlichen Strenge bereichert das Lernen bereits in der Sekundarstufe I und kann hitzige Diskussionen sowie Begriffsbildung in Gang setzen. Der Artikel demonstriert dies am Grenzwertbegriff und spannt dazu einen Bogen von der weiertsraßschen Monsterfunktion zu Phänomenen des mathematischen Schulalltags.
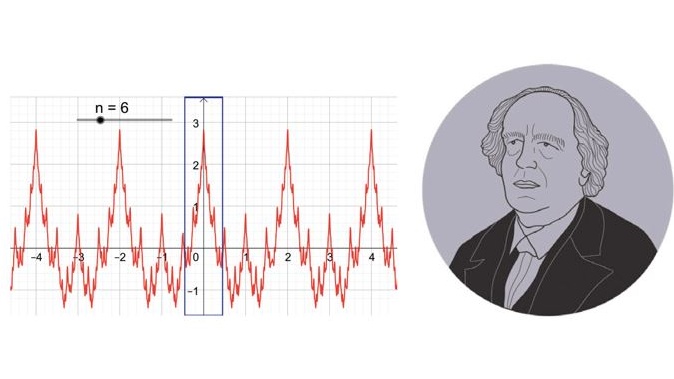


aus: Mathematik lehren Nr. 222 / 2020
Gesichter der Mathematik
-
- Unterricht (45-90 Min)
- Schuljahr 11-12
- Zugriff auf alle Inhalte deiner Fachzeitschriften
- 5 Downloads pro Kalendermonat
- Zugriff auf alle Inhalte deiner Fachzeitschriften
- unbegrenzte Downloads
- Podcasts
- Alle fachbezogenen Online-Seminare und Selbstlern-Online-Kurse
- Zugriff auf alle Inhalte deiner Fachzeitschriften
- unbegrenzte Downloads
- Podcasts
- Alle fachbezogenen Online-Seminare und Selbstlern-Online-Kurse
- Inkl. Friedrich+ Schule & Pädagogik
Du bist bereits Abonnent:in?
Teste unser digitales Angebot von Friedrich+ und erhalte
- Digitalen Vollzugriff auf die Inhalte der Zeitschrift Mathematik lehren
- Jährlich über 50 neue Beiträge mit Unterrichtseinheiten zu lehrplanrelevanten Themen
- Umfassendes Archiv mit über 175 didaktischen und fachwissenschaftlichen Beiträgen
Das digitale Angebot vom Friedrich-Verlag zu Mathematik lehren in der Sekundarstufe.
- 30 Tage Vollzugriff
- 3 Downloads inklusive
Alle Zeichen deuten darauf hin:
Du bist bereits Abonnent:in oder willst es werden?
Ich hoffe, ich konnte dir weiterhelfen. Hast du noch weitere Fragen? Chat neu starten
Deine Frage war nicht dabei? Das tut mir leid.
Wende dich gerne an unseren Kunden-Service. Du kannst dich telefonisch unter 051140004 150 und per E-Mail leserservice@friedrich-verlag.de melden oder das Kontaktformular nutzen.
Friedrich+ Mathematik - Jetzt 4 Wochen probelesen für nur 1 €
Jetzt testen
